グラフについて

グラフとは

～経路探索に必要なグラフの知識～


グラフ$G$とは，頂点（ノード）の集合$V$と，辺（枝，エッジ）の集合$E$によって定義され， \begin{equation} G=(V,E) \end{equation} と表す．つまり，グラフの本質は図形ではなく，あくまで「頂点と辺の集合」であるということである．

たとえば，$k$個の頂点$v_1,v_2,\cdots,v_k$があるとし，
$v_1$と$v_2$をつなぐ辺が$e_1$，$v_3$と$v_5$をつなぐ辺が$e_2\cdots$のように，$l$本の辺$e_1,e_2,\cdots,e_l$があるとすると， \begin{eqnarray} V&=&\{v_1,v_2,\cdots,v_k\}\\ E&=&\{e_1,e_2,\cdots,e_l\}\\ G&=&(V,E) \end{eqnarray} ということさえ情報として存在していれば，どのような図を描いたとしても本質としては同じグラフであるといってもよいことになる．

また，頂点の個数を$|V|$，辺の本数を$|E|$と表す．上の例では，$|V|=k,|E|=l$である．

有向グラフと無向グラフ

グラフには，辺に向きのない無向グラフと辺に向きがある有向グラフがある．

無向グラフにおいて，2つの頂点$v_i,v_j$をつなぐ辺を$(v_i,v_j)$と書くことにすれば，$(v_i,v_j)$と$(v_j,v_i)$は同じ辺を表す．
一方，有向グラフでは辺に向きがあるので，$v_i$から$v_j$へ向かう辺を$(v_i,v_j)$と書くことにすれば当然$(v_i,v_j)$と$(v_j,v_i)$は異なる辺を表すこととなる．

辺の重み

辺には重み（コスト）がある場合がある．このようなグラフは重みつきグラフやネットワークとよばれる．重みはふつう実数値で表され，場合に応じて様々な意味を持つ．
たとえば，交通ネットワークを表すグラフでは距離や運賃，所要時間などであり，為替のネットワークでは為替レート（に対応する値）などといったようなものであり，実際に負のコストを持つネットワークを考えることも十分ありうる．

グラフの表現方法

グラフを図に表せば，人が視覚的に把握することができるが，いざコンピュータにグラフを把握させようとすると図を入力するわけにもいかない．グラフには様々な表現方法があるのだが，その中でも特に簡単な隣接行列によるグラフの表現を説明する．
「行列」ではあるが，単に表現するだけであれば特に行列の知識は必要ない．
ただ，ここでは紹介しないが，行列の知識があれば隣接行列にもっと便利な性質があることを理解することもできるだろう．

また，アルゴリズムや考えたい性質によっては隣接行列以外の表現方法が有用のときもある．隣接リストによる表現や接続行列による表現など，様々な表現がある．これらはここでは説明しないが，すぐに理解できると思うので，自分で調べてみるとよい．

以下では，自己ループ（ある頂点から出て同じ頂点に戻ってくる辺）や重み$0$の辺は考えないものとする．

隣接行列による表現

無向グラフ

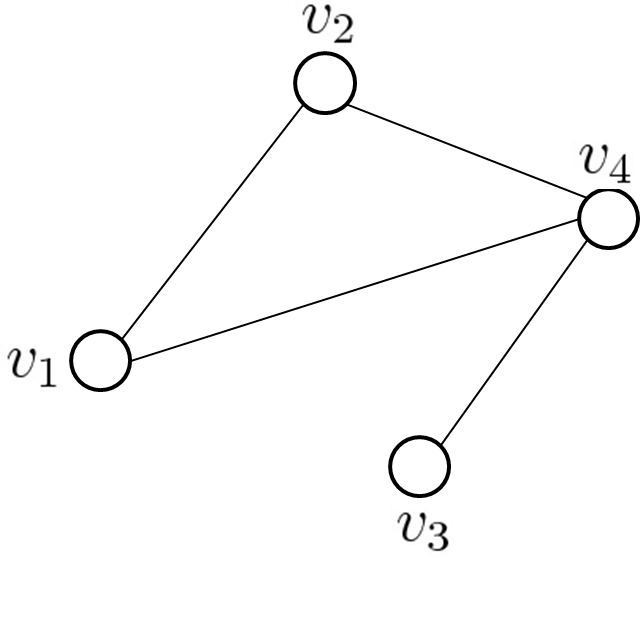
[図1]のグラフ$G=(V,E)$の$V,E$は \begin{eqnarray} V&=&\{v_1,v_2,v_3,v_4\}\\ E&=&\{e_{12},e_{14},e_{24},e_{34}\}\\ &&\mbox{（ただし，}e_{ij}\mbox{は}v_i\mbox{と}v_j\mbox{とをつなぐ辺）}\nonumber \end{eqnarray} のように定義されるが，次の[表1]のように表現することもできる．

＼	$v_1$	$v_2$	$v_3$	$v_4$
$v_1$	無	有	無	有
$v_2$	有	無	無	有
$v_3$	無	無	無	有
$v_4$	有	有	有	無

[表1]は，二つの頂点の間に辺があるかないかを「有」「無」で表している．ただ，[表1]のように「有」「無」のままではすこし扱いづらい．そこで，以下のように「有り」を$1$，「無し」を$0$と表すことで，次のような表現を得ることができる． \begin{equation} A = \left( \begin{array}{cccc} 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{array} \right) \end{equation} この行列$A$をグラフ$G$の隣接行列という．一般的に任意の無向グラフ$G$の隣接行列$A$は$|V|\times|V|$正方行列であり， \begin{eqnarray} A &=& (a_{ij})\\ a_{ij}&=&\left\{ \begin{array}{cl} 1 & (v_i\mbox{と}v_j\mbox{との間に辺}e_{ij}\mbox{がある場合}) \\ 0 & (v_i\mbox{と}v_j\mbox{との間に辺がない場合}) \end{array} \right. \end{eqnarray} と表現される．$a_{ij}$とは$A$の上から$i$行目，左から$j$列目の成分である．重み付きグラフの場合は，$1$の代わりに辺の重みを与えればよい．

重みのない無向グラフの隣接行列は対称行列（もとの行列$A$とその行と列を入れ替えてつくった行列$A^\mathrm{T}$とが等しい）である．

有向グラフ

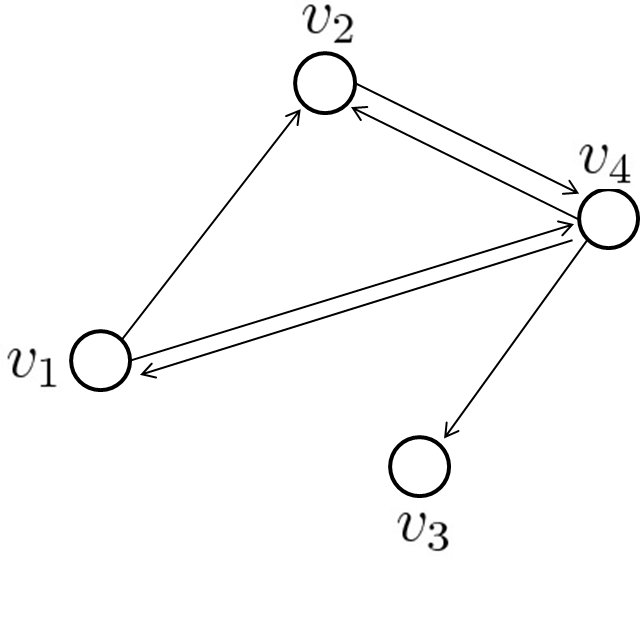
[図2]のグラフ$G=(V,E)$の$V,E$は \begin{eqnarray} V&=&\{v_1,v_2,v_3,v_4\}\\ E&=&\{e_{12},e_{14},e_{24},e_{41},e_{42},e_{43}\}\\ &&\mbox{（ただし，}e_{ij}\mbox{は}v_i\mbox{から}v_j\mbox{に向かう辺）}\nonumber \end{eqnarray} のように定義されるが，次の[表2]のように表現することもできる．

＼	$v_1$	$v_2$	$v_3$	$v_4$
$v_1$	無	有	無	有
$v_2$	無	無	無	有
$v_3$	無	無	無	無
$v_4$	有	有	有	無

[表2]は，左の頂点から上の頂点へ向かう辺があるかないかを「有」「無」で表している．ただ，[表2]のように「有」「無」のままではすこし扱いづらい．そこで，以下のように「有り」を$1$，「無し」を$0$と表すことで，次のような表現を得ることができる． \begin{equation} A = \left( \begin{array}{cccc} 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 \end{array} \right) \end{equation} この行列$A$をグラフ$G$の隣接行列という．一般的に任意の有向グラフ$G$の隣接行列$A$は$|V|\times|V|$正方行列であり， \begin{eqnarray} A &=& (a_{ij})\\ a_{ij}&=&\left\{ \begin{array}{cl} 1 & (v_i\mbox{から}v_j\mbox{へ向かう辺}e_{ij}\mbox{がある場合}) \\ 0 & (v_i\mbox{から}v_j\mbox{へ向かう辺がない場合}) \end{array} \right. \end{eqnarray} と表現される．重み付きグラフの場合は，$1$の代わりに辺の重みを与えればよい．