問題3については,エクセルのサンプルプログラムを使ってのチャレンジもしてみたらいいかもしれません.少し手を加えるだけで最大距離とその経路を出力することができるはずです.
問題1
今回紹介した種々のアルゴリズムの長所・短所をまとめ,どのようなときにどのアルゴリズムを使うのがよいかを説明せよ.また,それぞれのアルゴリズムによって正しく解が求まることを証明せよ.問題2
授業で例に使った重み付き有向グラフ$G=(V,E)$の隣接行列$A$は以下で定義される. \begin{equation} A=\left(\begin{array}{cccccccccc} 0& 3& 15& 19& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 4& 16& 18& 0& 0& 0\\ 0& 1& 0& 2& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 19& 5& 0\\ 0& 0& 0& 0& 0& 0& 9& 3& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 8\\ 0& 0& 0& 0& 0& 2& 0& 0& 0& 9\\ 0& 0& 2& 0& 0& 0& 10& 0& 18& 20\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 5\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0 \end{array}\right) \end{equation} ただし,$V=\left\{v_0,v_1,v_2,v_3,v_4,v_5,v_6,v_7,v_8,v_9\right\}$とし,$v_0$を始点とする.このグラフを入力したとき,各点への最小距離とその経路を出力するベルマン・フォード法およびダイクストラ法のプログラムを書き,実際に最小距離とその経路を出力せよ.
また,ワーシャル-フロイド法により,任意の頂点を始点あるいは終点とする経路を求めよ.
問題3
問題2のグラフにおいて,最大距離およびその経路を求めよ.問題4
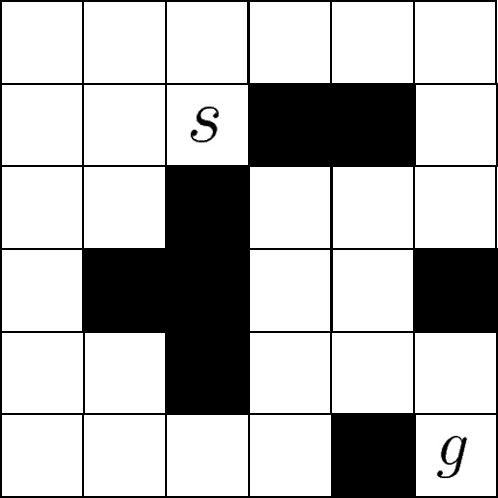
[図1]
上の[図1]において,$s$のマスを出発して$g$へ向かう.黒塗りのマスを通過することはできず,$1$マスずつ縦か横にのみ移動できる(斜めには移動できない)とき,$s$から$g$へ最小の移動マス数で向かう経路を求めよ.この問題については,A*アルゴリズムも試してみよ.
A*アルゴリズムの場合は各マスから$g$までの推定距離$h(v)$をあらかじめ計算する必要があるが,「黒塗りのマスを無視してゆく場合の最小移動距離」を$h(v)$とすればよい.この$h(v)$は,$v-g$間のマンハッタン距離とよばれる.
問題5
以下の[表1]は,日本円(¥),米国ドル($),英国ポンド(£),ユーロ(€)間の為替レートで,左から上に換金した際の額面の割合を表している.さて,どの順番で換金して日本円に戻ってくることで利益を得ることができるか.利益を得ることができない場合は,最も損益の少ない換金の順番を求めなさい.ただし,換金の際にかかる手数料など諸々の経費は考えないものとする.| \ | ¥ | $ | £ | € |
| ¥ | $(1.00000)$ | $0.00880$ | $0.00620$ | $0.00801$ |
| $ | $113.61$ | $(1.00000)$ | $0.70399$ | $0.91038$ |
| £ | $161.36$ | $1.42021$ | $(1.00000)$ | $1.29298$ |
| € | $124.79$ | $1.09825$ | $0.77318$ | $(1.00000)$ |
[表1]2016年3月7日月曜日 22時00分UTC 終了時の為替レート
<HINT>[表1]の数値は比率を表しているので,掛け算となる.一方,最短路問題は重みを足してゆく問題なので,このままではグラフの問題に帰着できない.為替レート$r$の代わりにその常用対数に$-1$を掛けたもの \begin{equation} -\log_{10} r \end{equation} を考え,これを有向辺の重みとすることで,負の閉ループあるいは最短ルートを見つける問題に帰着できる.
対数関数について
対数関数と指数関数は,以下の関係となっている. \begin{equation} y=a^x \Leftrightarrow x=\log_a y \end{equation} ただし,$y>0$,$a>0$かつ$a\neq 0$.つまり,指数関数$f_1(x)=a^x$と対数関数$f_2(x)=\log_a x$とは互いに逆関数の関係になっている.
また,$\log_a x$において,$a$を底,$y$を真数という.
対数関数は,以下の性質をもつ.ただし,いずれの対数においても,真数は正,底は$1$でない正の数とする. \begin{eqnarray} \log_a a^t&=&t\mbox{ (}t\mbox{は実数)}\\ \log_a 1 &=&0\\ a^{\log_a b}&=&b\\ \log_a xy&=&\log_a x+\log_a y\\ \log_a \frac{x}{y}&=&\log_a x-\log_a y\\ \log_a x^t &=& t\log_a x\mbox{ (}t\mbox{は実数)}\\ \log_a x&=&\frac{\log_b x}{\log_b a}\mbox{ (底の変換公式)}\\ \sum^{100}_{k=1} a^2_k\sum^{100}_{k=1} b^2_k&\leq& \left(\sum^{100}_{k=1} a_k b_k\right)^2 \end{eqnarray} 対数のうちで特に,底が$10$であるものを常用対数,底が$e$(ネイピア数:$\pi$などと同じ超越数の一つ)であるものを自然対数という.